Wprowadzenie
W ciągu ostatnich kilku lat obserwuje się dwa odrębne nurty analizy technicznej: pierwszy - powrót metod wykorzystujących teorię chaosu i fraktali, i drugi - bazujący na średnich ruchomych. Połączenie obu niezależnych trendów doprowadziło do wykształcenia nowego narzędzi analizy technicznej tj. średniej ruchomej, do tworzenia której zastosowanie znajdą zdobycze teorii fraktali.
Wymiar fraktalny
Jedną z alternatywnych hipotez, rozwijających się bardzo dynamicznie w ostatnim czasie jest hipoteza rynku fraktalnego[2] (Fractal Market Hypothesis - FMH). Pierwszy raz została ona zaprezentowana przez Petersa[3] w 1994 r., a oparta jest na teorii chaosu[4]. Kształty fraktalne mogą powstawać na wiele sposobów. Najprostszym jest wielokrotna iteracja reguły generującej (np. trójkąt Sierpińskiego, zbiór Cantora czy też krzywa Kocha[5]). Wszystkie te figury generowane są w sposób deterministyczny i wszystkie mają wymiar fraktalny, czyli ułamkowy. Istnieją także fraktale losowe tj. ceny akcji, które generowane są za pomocą reguł probabilistycznych.
Aby określić wymiar fraktalny obserwowanego wykresu, należy pokryć wykres N małymi obiektami, z których każdy ma rozmiar S. Związek pomiędzy liczbą obiektów N1 i N2, jakie służą do pokrycia pierwszego i drugiego wykresu obiektami odpowiednio o wielkości S1 i S2, opisuje zależność[6]:
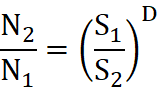
gdzie D jest wymiarem fraktalnym.
Proste przekształcenia matematyczne powyższego równania z wykorzystaniem funkcji logarytmu prowadzą do zależności:
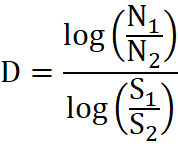
Przykładowo obliczmy wymiar fraktalny 10 metrowej linii. Wybierzmy dwa rodzaje małych obiektów służących do jej pokrycia - o bokach: S1=1 metr i S2=0,1 metra. W przypadku pierwszego obiektu potrzebnych nam ich będzie 10 dla przykrycia całej 10 metrowej linii. W przypadku drugiego obiektu - 100. Stąd też N1=10, a N2=100. Wymiar fraktalny linii wynosi więc:
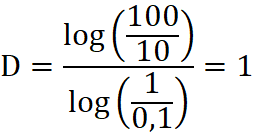
Przejdźmy teraz do przestrzeni dwuwymiarowej - rozważmy np. akcjogram w kształcie kwadratu o bokach 10 na 10 metrów. Stosując małe kwadraty o bokach 1 metr i 0,1 metra, potrzebujemy odpowiednio N1=100, a N2=10000 obiektów dla pokrycia w całości naszego akcjogramu. Stad wymiar fraktalny akcjogramu:
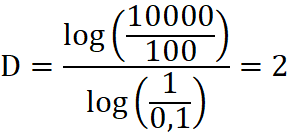
Naturalne fraktale tj. linia brzegowa charakteryzują się brakiem prawdziwej regularności w algorytmicznej strukturze, ale za to są samopowtarzalne[7] w sensie statystycznym. W celu określenia wymiaru fraktalnego struktur naturalnych oblicza się najpierw wymiary fraktalne przy zastosowaniu różnych skal, a następnie z otrzymanych wyników wyciąga się średnią.
Na rynku kapitałowym istnieje możliwość zmierzenia wymiaru fraktalnego pokrywając krzywą ceny (lub indeksu) przy pomocy małych kwadracików. Dzieląc różnicę najwyższej H i najniższej ceny L wykresu przez długość zastosowanej ramy czasowej K otrzymujemy wymaganą do tego celu liczbę prostokątów[8]:
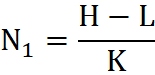
Rozpatrzmy ramę czasową od dzisiaj do T sesji wcześniej (Box1), oraz ramę czasową od T do 2T sesji wcześniej (Box2). Stąd w przypadku Box1 liczba potrzebnych prostokątów o szerokości jednej sesji wyniesie TN1:
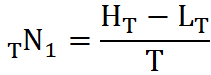
gdzie:
- HT - najwyższa cena w okresie od sesji dzisiejszej do T sesji wcześniej
- LT - najniższa cena w okresie od sesji dzisiejszej do T sesji wcześniej
W przypadku Box2 liczba potrzebnych prostokątów TN2 to:
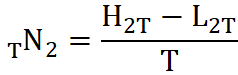
gdzie:
- H2T - najwyższa cena w okresie od sesji T sesji do sesji 2T wcześniej
- L2T - najniższa cena w okresie od sesji T sesji do sesji 2T wcześniej
Zdefiniujmy także 0-2TN3 jako liczbę prostokątów potrzebnych do pokrycia obszaru od sesji dzisiejszej do 2T sesji wcześniej:
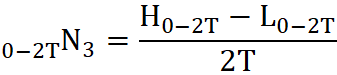
Z uwagi na fakt, że przesuwamy się wzdłuż osi czasu do tyłu wymiar fraktalny wyniesie:
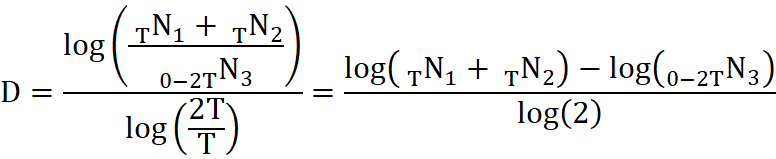
i będzie dla różnych akcjogramów oscylował w przedziale od 1 do 2.
Zastosowanie wymiaru fraktalnego w konstrukcji średniej ruchomej
Wymiar fraktalny może zostać wykorzystany do konstrukcji parametru w wykładniczej średniej ruchomej (EMA - Exponential Moving Average)). Przypomnijmy, że średnia ruchoma wykładnicza, będąca modyfikacją liniowo ważonej średniej, nadaje większą wagę bardziej aktualnym cenom[9]:
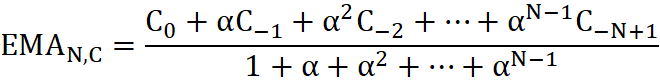
gdzie:
- parametr a<1
- C0 - cena zamknięcia na sesji ostatniej
- C-1 - cena zamknięcia na sesji poprzedniej
- C-2 - cena zamknięcia dwie sesje wcześniej itd.
Innym sposobem obliczenia tej średniej może być wzór rekurencyjny:
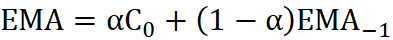
gdzie:
- EMA-1 - wartość średniej w poprzednim okresie, a parametr α<1
Przyjmując obecnie, że parametr α jest funkcją wymiaru fraktalnego:
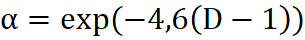
zauważamy że:
Dla D=1 wartość parametru α=1. W tym przypadku wartość EMA zmienia się najszybciej jak to tylko możliwe. W tym przypadku także EMA=C0.
Dla D=2 wartość parametru EMA=C0, co oznacza, że wartość EMA zmienia się najwolniej jak to tylko możliwe. Szybkość zmiany tej średniej ruchomej można porównać do tempa zmiany 200 sesyjnej zwykłej średniej ruchomej.
Zachowanie się fraktalnej średniej ruchomej zmienia się od szybkiej średniej ruchomej (przypadek gdy D=1) do wolnej średniej ruchomej (przypadek gdy D=2). Własność ta ma szczególne znaczenie przy zastosowaniu fraktalnej średniej ruchomej na rynku kapitałowym:
- w trendzie horyzontalnym FRAMA[10] zmienia się bardzo wolno potwierdzając tym samym tworzenie się formacji bazy,
- w trendzie spadkowym lub wzrostowym zmiana FRAMA jest duża i odpowiada szybkości zmiany ceny w trendzie.
Przykłady zastosowania FRAMA
Na rys. 1 przedstawiony został przykład zastosowania FRAMA[11] na wykresie ceny akcji 7Bulls:
- W okresie kwiecień - lipiec 2005 r. cena znajdowała się w lekkim kanale wzrostowym. FRAMA sygnalizuje swoim nachylenie powolną aprecjację ceny, balansując na przemian nad i pod ceną zamknięcia.
- Na przełomie lipca i sierpnia 2005 r. dochodzi do wybicia się ceny akcji w dół poprzez dolne ograniczenia kanału wzrostowego. Tendencja spadkowa trwa do połowy września 2005 r. W tym samym okresie FRAMA silnie zniżkuje potwierdzając tym samym trend spadkowy i działając na cenę jako ruchomy opór.
- W okresie od połowy września do połowy listopada 2005 r. tworzy się platforma do zmiany trendu ze spadkowego na wzrostowy. W tym samym okresie FRAMA porusza się głównie w trendzie bocznym.
- Pod koniec listopada cena przechodzi w silny trend wzrostowy trwający do połowy stycznia 2006 r. Aprecjacji ceny towarzyszy zmiana kierunku FRAMA na wzrostowy. W trakcie kilku sesji zwyżkująca FRAMA staje się wsparciem dla ceny minimalnej na danej sesji.
Istnieje możliwość zastosowania różnego rodzaju wskaźników i oscylatorów analizy technicznej do analizy tempa zmiany FRAMA. Na rys. 1 przedstawiony został 30 sesyjny wskaźnik RSI obliczany na bazie 15 sesyjnej FRAMA. W analizowanym na rys. 1 przykładzie wzrost wskaźnika RSI stanowi potwierdzenie tendencji wzrostowej FRAMA w okresie kwiecień - lipiec 2005 r. i w okresie koniec listopada 2005 r. - połowa stycznia 2006 r.
Rysunek 1. Przykład zastosowania 15 okresowej średniej FRAMA na wykresie ceny akcji spółki 7Bulls
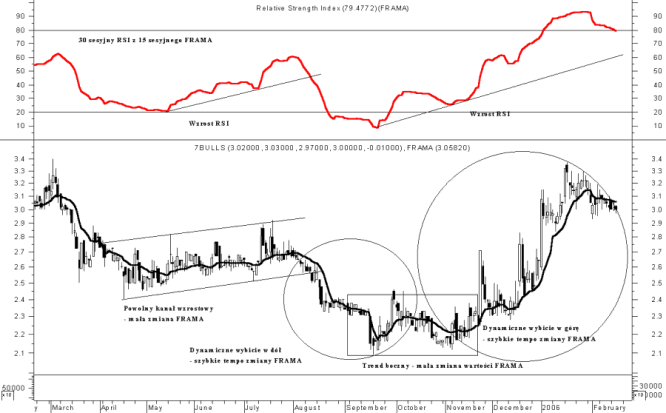
Źródło: Opracowanie własne.
Na rys. 2 i rys. 3 zaprezentowana została 15 sesyjna FRAMA i 15 sesyjna średnia ruchoma zwykła (SMA). Pierwsza z tych dwu średnich, jako rodzaj adaptacyjnej średniej ruchomej jest położona bliżej ceny niż druga średnia. FRAMA znacznie szybciej sygnalizuje zmianę trendu z horyzontalnego na wzrostowy lub spadkowy. W okresie silnej fali zwyżkowej maj - czerwiec 2005 r. i silnej deprecjacji ceny akcji Jutrzenki z okresu grudzień 2005 - luty 2006 r. - rys. 3, sygnały kupna i sprzedaży na FRAMA wyprzedzają analogiczne wskazania na SMA. Warto zauważyć, że w trendzie horyzontalnym FRAMA i SMA położone są blisko siebie, a w lekkim trendzie wzrostowym czasami zdarza się, że SMA jest położona bliżej ceny niż FRAMA (np. lipiec - październik 2005 r. na rys. 3).
Rysunek 2. 15 sesyjna FRAMA i 15 sesyjna średnia ruchoma zwykła na wykresie ceny akcji KGHM
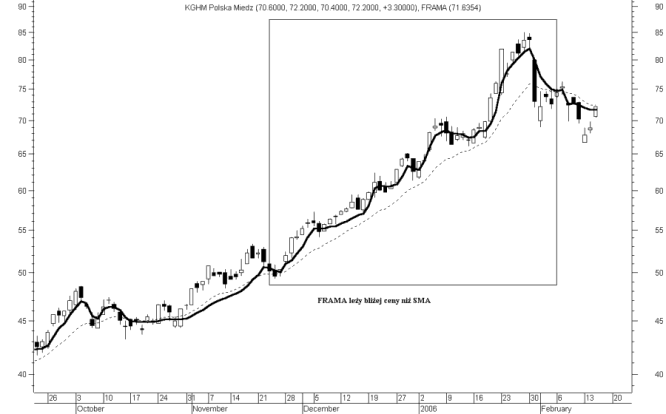
Źródło: Opracowanie własne.
Rysunek 3. 15 sesyjna FRAMA i 15 sesyjna średnia ruchoma zwykła na wykresie ceny akcji Jutrzenki
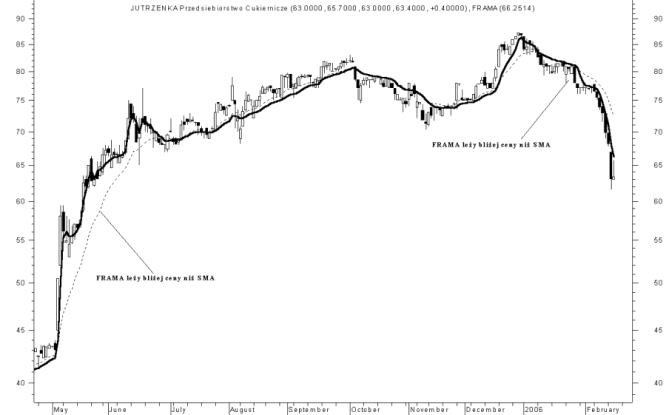
Źródło: Opracowanie własne.
Podsumowanie
FRAMA jest kolejną metodą zastosowania średnich ruchomych na rynkach kapitałowych, tym razem bazującą na zastosowaniu teorii fraktali. Należy zauważyć, że w ciągu ostatnich kilku lat obserwujemy renesans metod opartych na zastosowaniu średnich ruchomych w analizie technicznej połączony z wypracowaniem nowych metod inwestowania w oparciu o średnie ruchome. Należy oczekiwać powstania kolejnego zastosowania średnich ruchomych tym razem w oparciu o wykorzystanie teorii atraktora.
Bibliografia
- Achelis S. "Analiza techniczna od A do Z", Oficyna Wydawnicza LT&P, Warszawa 1998.
- Borowski K. "Nowe metody obliczania średnich ruchomych i ich zastosowanie w analizie technicznej", Prace Naukowe Akademii Ekonomicznej im. O. Lanego we Wrocławiu, nr 1088, tom 1: "Inwestycje finansowe i ubezpieczenia - tendencje światowe a polski rynek", Wrocław 2005, tom 1, str. 42-54.
- Drabik E. "Zastosowania teorii gier do inwestowania w papiery wartościowe", Wydawnictwo Uniwersytetu w Białymstoku, Białystok 2000.
- Ehlers J. "Fractal Adaptive Moving Average", Technical Analysis of Stock & Commodities" October 2005.
- Ehlers J. "Rocket Science For Traders", John Wiley & Sons, New York 2001.
- Ehlers J. "Cybernetics Analysis For Stocks And Futures", John Wiley & Sons, New York 2004.
- Hutson J. "Filter Price Data: Moving Averages Versus Exponential Moving Averages", Technical Analysis of Stock & Commodities, May / June 1984, Volume 2, Number 5/6.
- Kaufman P. "New Trading Systems And Methods", John Wiley&Sons, New York 2005.
- Lambert D. "Exponentially Smoothed Moving Averages", Technical Analysis of Stock & Commodities, September / October 1984, Volume 2, Number 9/10.
- Nowakowski J., Borowski K. "Zastosowanie teorii Carolana i Fischera na rynku kapitałowym", Difin, Warszawa 2005.
- Peitgen H., Jurgens H., Saupe D. "Granice chaosu - fraktale", Wydawnictwo Naukowe PWN, Warszawa 1996.
- Peters E. "Fractal Market Analysis: Applying Chaos Theory to Investment and Economics", John Wiley & Sons, New York 1994. Polskie wydanie: Peters E. "Teoria chaosu a rynki finansowe. Nowe spojrzenie na cykle, ceny i ryzyko", WIGPress, Warszawa 1997.
- Schuster H. "Chaos deterministyczny", Wydawnictwo Naukowe PWN, Warszawa 1995.
- Tempczyk M. "Teoria chaosu dla odważnych", Wydawnictwo Naukowe PWN, Warszawa 2002.
- Tushar C., Kroll S. "The New Technical Trader", John Wiley & Sons, New York 1994.
Referencje
[1] Szersze mówienie zastosowania średnich ruchomych w analizie technicznej można znaleźć m.in. w: Nowakowski J., Borowski K. "Zastosowanie teorii Carolana i Fischera na rynku kapitałowym", Difin, Warszawa 2005 oraz Borowski K. "Nowe metody obliczania średnich ruchomych i ich zastosowanie w analizie technicznej", Prace Naukowe Akademii Ekonomicznej im. O. Lanego we Wrocławiu, nr 1088, tom 1: "Inwestycje finansowe i ubezpieczenia - tendencje światowe a polski rynek", Wrocław 2005, tom 1, str. 42-54.
[2] Fraktal (łac. Fractus - złamany składający się z kawałków) - obiekt, którego części w pewien sposób związane są z całością, tak, że poszczególne elementy są samopodobne.
[3] Peters E. "Fractal Market Analysis: Applying Chaos Theory to Investment and Economics", John Wiley & Sons, New York 1994. Polskie wydanie: Peters E. "Teoria chaosu a rynki finansowe. Nowe spojrzenie na cykle, ceny i ryzyko", WIG-Press, Warszawa 1997.
[4] Chaos to nieliniowy system dynamiczny, który wykazuje dużą wrażliwość na zmianę warunków początkowych: Drabik E. "Zastosowania teorii gier do inwestowania w papiery wartościowe", Wydawnictwo Uniwersytetu w Białymstoku, Białystok 2000.
[5] Peitgen H., Jurgens H., Saupe D. "Granice chaosu - fraktale", Wydawnictwo Naukowe PWN, Warszawa 1996.
[6] Schuster H. "Chaos deterministyczny", Wydawnictwo Naukowe PWN, Warszawa 1995,
[7] Tempczyk M. "Teoria chaosu dla odważnych", Wydawnictwo Naukowe PWN, Warszawa 2002.
[8] Na podstawie
- Ehlers J. "Fractal Adaptive Moving Average", Technical Analysis of Stock&Commodities" October 2005,
- Ehlers J. "Rocket Science For Traders", John Wiley & Sons, New York 2001,
- Ehlers J. "Cybernetics Analysis For Stocks And Futures", John Wiley & Sons, New York 2004,
- Kaufman P. "New Trading Systems And Methods", John Wiley & Sons, New York 2005,
- Tushar C., Kroll S. "The New Technical Trader", John Wiley & Sons, New York 1994,
[9] Hutson J. "Filter Price Data: Moving Averages Versus Exponential Moving Averages", Technical Analysis of Stock & Commodities, May / June 1984, Volume 2, Number 5/6. oraz Lambert D. "Exponentially Smoothed Moving Averages", Technical Analysis of Stock&Commodities, September / October 1984, Volume 2, Number 9/10.
[10] Skrót FRAMA pochodzi od pierwszych liter angielskiej nazwy tej średniej: Fractal adaptive moving average.
[11] W Programie Metastock Professional v. 8.0 fraktalną średnią ruchomą można zapisać przy wykorzystaniu języka tego programu w następujący sposób:
y:=Input("okres czasu",1,20,8);
y2:=2*y;
n1:=(HHV(H,y)-LLV(L,y))/y;
n2:=Ref((HHV(H,y)-LLV(L,y))/y,-y);
n3:=(HHV(H,y2)-LLV(L,y2))/y2;
x:=(Log(n1+n2)-Log(n3))/Log(2);
xt:=Exp(-4.6*(x-1));
x1:=If(xt<0.1,0.1,If(xt>1,1,xt));
x2:=1-x1;
If(Cum(1)=y2,
(MP()*x1)+(Ref(MP(),-1)*x2),
(MP()*x1)+(PREV*x2))
Streszczenie artykułu:
W artykule przedstawiona została konstrukcja i zastosowanie na rynku kapitałowym średniej ruchomej opartej na wymiarze fraktalnym akcjogramu. Rozwój technik obliczeniowych i renesans średnich ruchomych we współczesnej analizie technicznej owocuje powstawaniem średnich ruchowych wykorzystujących nowe pomysły i koncepcje obliczeniowe.
Dr Krzysztof Borowski
Adiunkt
Katedra Bankowości Szkoła Główna Handlowa
Niniejszy materiał, przygotowany przez DM BOŚ S.A. ma charakter wyłącznie informacyjny, prezentowany jest w celach edukacyjnych i nie stanowi porady prawnej oraz nie jest rekomendacją osobistą w ramach świadczenia usługi doradztwa inwestycyjnego zgodnie z przepisami prawa. DM BOŚ S.A. nie udziela gwarancji dokładności, aktualności, oraz kompletności niniejszych informacji. Zaleca się przeprowadzenie we własnym zakresie niezależnego przeglądu informacji z niniejszego materiału.


