W każdej chwili na rynku działa wiele formacji cenowych. W typowej analizie cykli 30-tygodniowy cykl może być wzrostowy, podczas gdy 30-miesięczny znajduje się w fazie spadkowej, a analitycy szukają punktów, kiedy większość cykli krótko i średnioterminowych jest zsynchronizowana razem w krótkim okresie czasu, tj. wtedy gdy górki i dołki obu cykli pokrywają się. W ermanometrii poszukuje się również takich punktów, w których przecina się jednocześnie kilka formacji (schematów) rozwojowych. Analiza klasyczna przyjmuje założenie, że rynek rozwija się wyłącznie w kierunku przyszłości. Nowy cykl rozpoczyna się tam, gdzie stary się kończy. Ermanometria uważa, że czas rynkowy ma strukturę sferyczną i jest wielowymiarowy. Dopuszcza zatem istnienie spirali logarytmicznych wielowymiarowych.
Rysunek 1. Spirala logarytmiczna trójwymiarowa - czas płynie na osi k
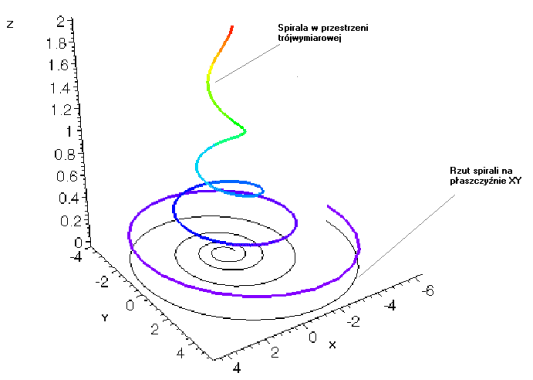
Źródło: opracowanie własne na podstawie strony internetowej http://arnold.usno.navy.mil/murison/
z dnia 22.06.2002
Segmenty wzrostowe są ciągłe, ale z uwagi na swoją wielowymiarowość ich odwzorowania na płaszczyźnie są skośne czy też nieco przesunięte w stosunku do ich rzeczywistej odległości w wielowymiarowej przestrzeni. Paradoksalnie, dwa sąsiadujące segmenty mogą być oddzielone znaczną odległością w momencie ich zrzutowania na płaszczyznę. Ten paradoks najlepiej ilustruje przykład płaskiej mapy, owiniętej wokół Ziemi. Jest oczywistym, że mapa nie pasowałaby dokładnie do obszaru, który przecież reprezentuje.
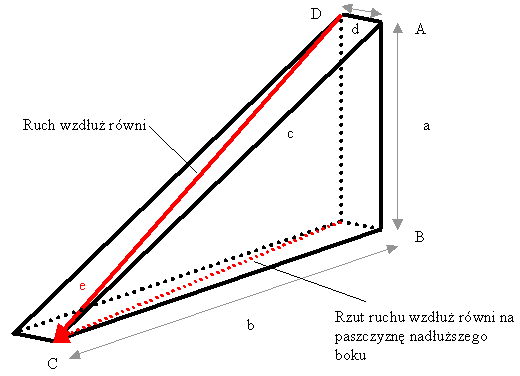
Wyobraźmy sobie, że konstruujemy równię pochyłą o bokach (rysunek 2):
- wysokość - odcinek AB o długości a
- szerokość - odcinek AD o długości d
- długość drugiej przyprostokątnej - odcinek BC o długości b będący sumą odcinków: AB i AD: b = a + d
- długość przeciwprostokątnej - odcinek AC o długości c wynikającej z twierdzenia Pitagorasa: c2 = a2 + b2 = 2a2 + d2 + 2ad
- długość przeciwprostokątnej na równi pochyłej - odcinek DC o długości e wynikającej z twierdzenia Pitagorasa: e2 = c2 + d2 = 2a2 + 2d2 + 2ad
Rysunek 2. Ruch rynku w przestrzeni wielowymiarowej
Źródło: opracowanie własne na podstawie strony internetowej http://arnold.usno.navy.mil/murison/ z dnia 22.06.2002
Ruch rynku wzdłuż równi pochyłej zrzutowany na płaszczyznę najdłuższego boku wyglądałby jak odcinek prosty. Tak właśnie widzimy go na stosowanym w analizie technicznej akcjogramie. W rzeczywistości jest on wycinkiem pewnej wielowymiarowej sfery czasowej.
Przykład 1
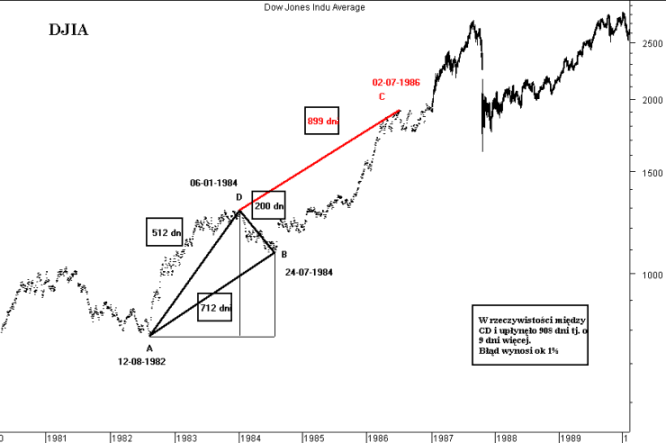
Przyjmując za punkty zwrotne A, B, D lokalne ekstrema indeksu DJIA (rysunek 3)- stosując metodę opisaną powyżej, jesteśmy w stanie obliczyć datę punktu zwrotnego C. Potencjalny punkt zwrotny indeksu wypada 02.07.1986 r. W rzeczywistości szczyt indeksu przypadł 9 dni później - 11.07.1986 r.
Rysunek 3. Wyznaczanie punktów zwrotnych w przyszłości na podstawie trzech punktów zwrotnych tj. dwóch odcinków, na przykładzie dziennego wykresu Dow Jones Industrial Average (DJIA)
Źródło: opracowanie własne
Tabela 1. Przykład zastosowania ermanometrii do wyznaczania puntków zwrotnych
1982-08-12
Data2
Liczba dni
Odcinek
1984-01-06
512
a
1984-01-06
Data2
Liczba dni
Odcinek
1984-07-24
200
d
1982-08-12
Data2
Liczba dni
Odcinek
1984-07-24
712
b
1984-01-06
Data2
Liczba dni
Odcinek
1986-07-02
899
e
| Data1 | Data2 | Liczba dni | Odcinek |
|---|---|---|---|
| 1982-08-12 | 1984-01-06 | 512 | a |
| 1984-01-06 | 1984-07-24 | 200 | d |
| 1982-08-12 | 1984-07-24 | 712 | b |
| 1984-01-06 | 1986-07-02 | 899 | e |
Źródło: opracowanie własne
Przykład 2
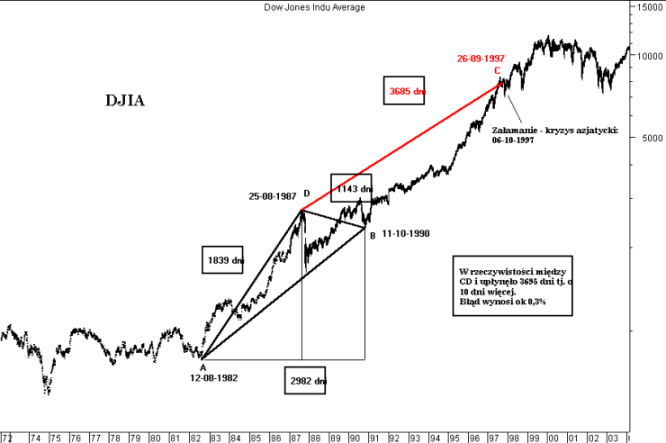
Drugi przykład obliczenia punktu zwrotnego C na podstawie wybranych punktów A, B i D (szczyt indeksu DJIA z drugiego największego krachu na Wall Street) został przedstawiony poniżej. Potencjalny punkt zwrotny został wyznaczony na 26.09.1997 r. W rzeczywistości szczyt indeksu giełdy amerykańskiej przypadł 10 dni później i stanowił lokalne ekstremum przed załamaniem po kryzysie azjatyckim.
Rysunek 4. Wyznaczanie punktów zwrotnych w przyszłości na podstawie trzech punktów zwrotnych tj. dwóch odcinków, na przykładzie dziennego wykresu Dow Jones Industrial Average (DJIA)
Źródło: opracowanie własne
Tabela 2. Przykład zastosowania ermanometrii do wyznaczania punktów zwrotnych
1982-08-12
Data2
Liczba dni
Odcinek
1987-08-25
1839
a
1987-08-25
Data2
Liczba dni
Odcinek
1990-10-11
1143
b
1982-08-12
Data2
Liczba dni
Odcinek
1990-10-11
2982
d
1987-08-25
Data2
Liczba dni
Odcinek
1997-09-26
3685
e
| Data1 | Data2 | Liczba dni | Odcinek |
|---|---|---|---|
| 1982-08-12 | 1987-08-25 | 1839 | a |
| 1987-08-25 | 1990-10-11 | 1143 | b |
| 1982-08-12 | 1990-10-11 | 2982 | d |
| 1987-08-25 | 1997-09-26 | 3685 | e |
Źródło: opracowanie własne
Wydaje się zatem słusznym, aby ruchy cen obserwować z perspektywy sfer obracających się zgodnie lub przeciwnie do ruchu wskazówek zegara. W ten sposób istnieje szansa na odkrycie struktur normalnie niewidocznych w dwuwymiarowej przestrzeni standardowego akcjogramu. W tej nowej przestrzeni czasowe ruchy giełdowe są reprezentowane przez takie figury (schematy) jak: okręgi, trójkąty lub serie nieciągłych linii prostych2.
Perspektywa sferyczna wymaga, aby widzieć czas jako obracający się i odnawialny, a analiza ruchów sfer, a w szczególności wielowymiarowych spiral obracających się zgodnie z kierunkiem zegara i przeciwnie doń, pozwala uzyskać wiele wzorów nieobserwowalnych na płaszczyźnie oraz ukrytych symetrii.
Podstawowe zasady przy stosowaniu ermanometrii na rynku amerykańskim:
- Ekstrema cenowe osiągane są w czasie notowań ciągłych. Ceny zamknięcia mają znaczenie drugorzędne
- Jednostką pomiaru czasu jest kwadrans. Największą jednostką czasu stosowaną przez tę technikę jest dzień. Nie stosuje się pomiaru czasu w tygodniach czy miesiącach
- Sygnały wygenerowane przez S&P muszą się potwierdzać z wskazaniami Dow Jones Industrial Average w przeciągu dwu dni sesyjnych (szczegóły dotyczące pokrywania się sygnałów od obu indeksów można znaleźć w pracy: Erman W. "Log Spirals in the Stock Market"3.). Podkreślmy, że jest to wymóg bardzo zbliżony do teorii Dowa, chociaż o wiele bardziej zaostrzony pod względem czasu potwierdzenia. W przypadku tej ostatniej teorii potwierdzenie między DJIA i DJTA powinno nastąpić od jednego tygodnia do trzech miesięcy
- Odstęp czasu pomiędzy dwoma ważnymi punktami zwrotnymi jest oddzielnym i odrębnym ruchem, nawet jeśli zawiera w sobie inny istotny ruch rynku
- Tylko dwa ruchy (tzw. podstawowe) są konieczne do ustalenia stałych spirali logarytmicznej i prostokątnej (wielokątnej). Przy czym jednocześnie wykorzystuje się spirale rozwijające się zgodnie i przeciwnie do ruchu wskazówek zegara
Do wyznaczania punktów zwrotnych w przyszłości wykorzystuje się logarytmiczną spiralę prostokątną. Dokonuje się tego w następujących krokach4:
- ustalenie relacji między dwoma odcinkami bazowymi - np. 497 i 362 dni (przykład teoretyczny). Relacje te wynoszą c=497/362 = 1,37293 i l=1/1,37293 = 1/c = 0,72836
- narysowanie logarytmicznej spirali prostokątnej z dwoma odcinkami bazowymi 362 i 497 dni
- Obliczenie pozostałych odcinków spirali otrzymujemy jako iloczyn liczb 497 i odpowiedniej potęgi współczynnika relacji. Dla spirali rozwijającej się mamy zatem:
497 . 1,37293 = 682,35
497 . 1,372932 = 682,35 . 1,37293 = 936,81 etc.
Analogicznie postępujemy w przypadku spirali zwijającej się - wtedy do obliczeń wykorzystujemy odpowiednie potęgi relacji l = 0,72836.
W ten sposób możemy odtworzyć wszystkie odcinki spirali rozwijającej się:
139,88 192,05 263,67 362,00 497,00 682,35 936,81 1286,17 1765,83
Zgodnie z teorią dni docelowe można uzyskać także poprzez sumowanie odcinków poziomych i pionowych prostokątnej spirali logarytmicznej.
Metody wykorzystania przez ermanometrię trójkątów wewnątrz prostokątnej spirali logarytmicznej, zastosowanie okręgów i innych figur można znaleźć w książce W. Ermana5. Należy zauważyć, że teoria dopuszcza stosowanie dowolnych relacji (współczynników) φ w równaniu określającym spiralę logarytmiczną: r = eqψ. Jeśli za ψ podstawimy stałą Fibonacciego Φ otrzymamy spirale wykorzystywane przez teorie: fal Elliotta, okienek Carolana i Fischera.
Więcej na temat ermanometrii znajduje się w książce J. Nowakowski, K. Borowski "Zastosowania teorii Carolana i Fischera na rynku kapitałowym, Difin 2004."
Referencje
- Erman W. "Ermanometry: the Perfectly Patterned Markets", Ermanometry Research, Nashville 1999
- Erman W. "Ermanometry: the Perfectly Patterned Markets", Ermanometry Research, Nashville 1999
- Erman W. "Log Spirals in the Stock Market", Technical Analysis of Stock & Commodities, February 1999, Volume 17, Number 2, str. 20
- Erman W. "Compound Pivots and Market Symmetry", Technical Analysis of Stock & Commodities, April 1999, Volume 17, Number 4
- Erman W. "Ermanometry: the Perfectly Patterned Markets", Ermanometry Research, Nashville 1999
Niniejszy materiał, przygotowany przez DM BOŚ S.A. ma charakter wyłącznie informacyjny, prezentowany jest w celach edukacyjnych i nie stanowi porady prawnej oraz nie jest rekomendacją osobistą w ramach świadczenia usługi doradztwa inwestycyjnego zgodnie z przepisami prawa. DM BOŚ S.A. nie udziela gwarancji dokładności, aktualności, oraz kompletności niniejszych informacji. Zaleca się przeprowadzenie we własnym zakresie niezależnego przeglądu informacji z niniejszego materiału.


