Wprowadzenie
Wiele metod statystycznych stosowanych w analizie technicznej i wykorzystujących do pomiaru ryzyka odchylenie standardowe przyjmuje milczące założenie, że rozkład zmian cen akcji (lub innych aktywów)[1] na giełdzie papierów wartościowych jest rozkładem normalnym (gaussowskim). Można spotkać prace statystyczne dowodzące, że w istocie rozkład zmian cen nie jest rozkładem normalnym[2].
Transformata Fishera jest prostym zabiegiem matematycznym przekształcającym zbiór danych wejściowych w zbiór, którego funkcją gęstości prawdopodobieństwa jest funkcją gęstości rozkładu normalnego. Po jednokrotnym zastosowaniu transformaty Fishera, w zbiorze wynikowym mogą być stosowane wszystkie metody statystyczne odpowiednie dla rozkładu normalnego. Do ciekawych wniosków prowadzi także zastosowanie odwrotnej transformaty Fishera.
Zwykła transformata Fishera
Zwykłą transformatę Fishera możemy przedstawić w sposób następujący:
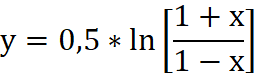
Równanie 1
gdzie:
- x - sygnał wejściowy
- y - sygnał wyjściowy
Rysunek 1. Przykład transformaty Fishera dla sygnałów X z przedziału <-1,1>
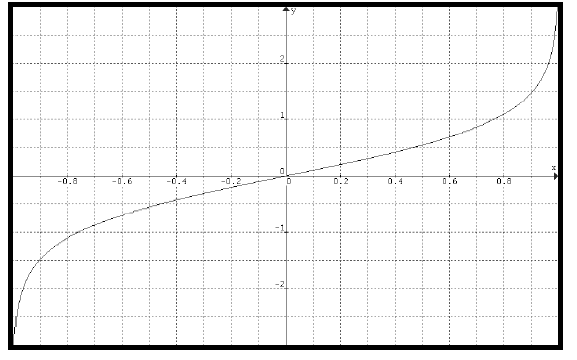
Źródło: opracowanie własne.
W przypadku kiedy sygnał wejściowy x jest bliski wartości przeciętnej, wtedy wartość sygnału wyjściowego y jest bliska wartości x. Jako przykład rozpatrzymy sytuację, gdy x=0,5, wtedy wartość y jest nieznacznie większa od 0,5. Dokładnie wynosi ona 0,54931. W przypadku, gdy wartość sygnału wejściowego jest bliska którejś z wartości skrajnych tj. -1 lub 1, wtedy wartość sygnału wyjściowego jest znacznie większa od wartości x. W ten sposób następuje wzmocnienie wielkości sygnału wyjściowego. Można pokazać[3], że otrzymana w wyniku zastosowania transformaty Fishera dla rozkładu sinusoidalnego (sygnał wejściowy) gęstość rozkładu prawdopodobieństwa jest zbliżona do gęstości prawdopodobieństwa rozkładu normalnego. W literaturze przedmiotu przyjęto określać taki stan jako "prawie" gaussowski. Gęstości obu rozkładów tj. sinusoidalnego i "prawie" gaussowskiego są równe w punkcie x=0.
Rysunek 2. Transformata Fishera rozkładu sinusoidalnego ma rozkład zbliżony do gaussowskiego
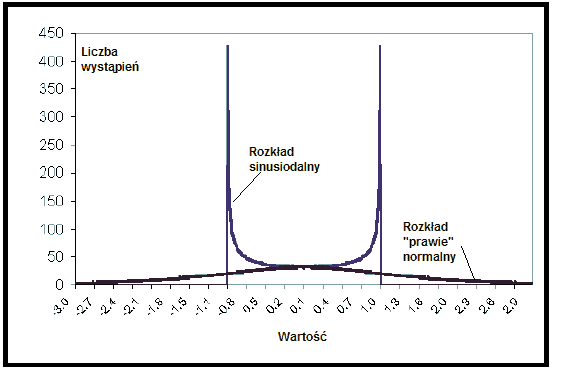
Źródło: opracowanie własne.
Jeśli teraz wybierzemy określoną ramę czasową (np. horyzont 14 lub 30 sesyjny) i dokonamy rozkładu zmian stóp procentowych wybranego aktywu (lub rozkładu częstości występowania poszczególnych cen tego aktywu), a następnie przeprowadzimy proces normalizacji tego rozkładu, tak aby sygnał wejściowy należał do przedziału <-1,1>, a w dalszej kolejności poddamy sygnał wejściowy transformacie Fishera, to okaże się że ekstremalne zmiany ceny aktywu występują niezwykle rzadko. W ten sposób analitycy mogą wskazać istotne punkty zwrotne na wykresie ceny analizowanego aktywu.
Przykład transformaty Fishera został przedstawiony na rys. 3 - okno drugie od góry. Punkty zwrotne ceny akcji KGHM przy zastosowaniu transformaty są jeszcze lepiej widoczne - transformata tworzy wyraźne szczyty lub dołki szybko reagując na zmianę tendencji. Linią przerywaną zaznaczona została wartość transformaty z poprzedniej sesji - w ten sposób przebicie przez transformatę jej uprzedniej wartości może być wykorzystane w budowie systemów transakcyjnych jako sygnał kupna lub sprzedaży. Dodatkowo można na wykresie transformaty zaznaczyć, podobnie jak w przypadku niektórych wskaźników, poziomy wykupienia i wyprzedania sugerujące możliwość zmiany trendu na przeciwny (punkty: 3, 4, 5 i 6). Przekroczenie poziomów wykupienia lub wyprzedania należy uznać za stan skrajny.
Rysunek 3. Przykład zastosowania transformaty Fishera 14 dniowej na wykresie ceny akcji KGHM
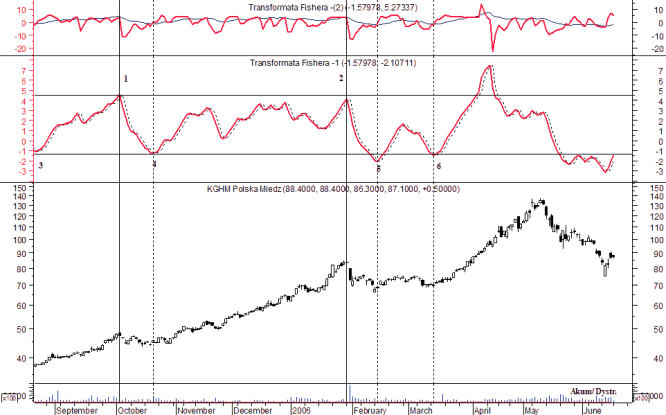
Okno czasowe - 10 sesji, transformowana jest cena średnia
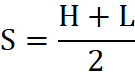
gdzie:
- H i L oznaczaną odpowiednio najwyższą i najniższą cenę w trakcie sesji.
Źródło: opracowanie własne.
Do transformaty Fishera można wykorzystać także jako sygnał wejściowy wartość oscylatora lub wskaźnika używanego w analizie technicznej. Na rys. 4 przedstawiona została transformata Fishera z oscylatora MACD[4], a na rys. 3 z oscylatora ROC (okno pierwsze od góry). Na wykresie transformaty powstały także formacje stosowane w klasycznej analizie technicznej:
- Podwójny szczyt (oznaczony jako pkt 2) - drugi szczyt transformaty MACD zbiegł się z sygnałem sprzedaży na MACD. Wcześniejszy szczyt transformaty nie został potwierdzony przez szczyt oscylatora.
- Podwójne dno - sygnalizacja końca korekty spadkowej i początek nowej fali wzrostów z okresu marzec - maj 2006 r.
- Negatywna dywergencja - ostrzeżenie przed korektą spadkową styczeń - marzec 2006 r. Trzeci kolejny szczyt w formacji negatywnej dywergencji pokrył się ze szczytem transformaty Fishera z ceny przeciętnej obliczonej przy zastosowaniu okna 30 sesyjnego.
Warto odnotować fakt, że zmiana horyzontu czasowego liczenia transformaty Fishera dla ceny przeciętnej z 10 na 30 sesji dobrze sygnalizowała dwa szczyt ceny akcji KGHM z października 2005 r. (punkt 4) i stycznia 2006 r. (punkt 5).
Rysunek 4. Przykład zastosowania transformaty Fishera dla oscylatora MACD
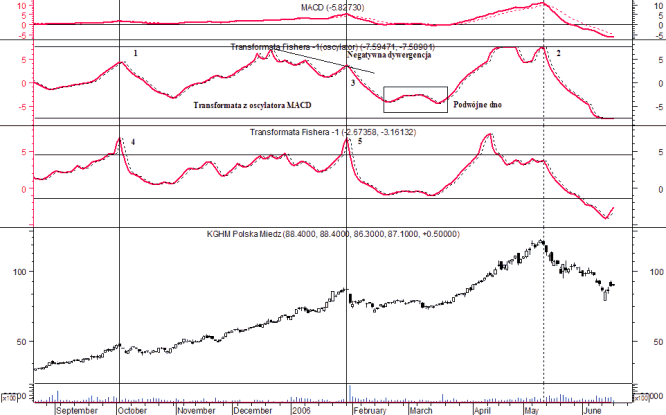
Źródło: opracowanie własne.
Okno czasowe - 30 sesji, transformowany jest oscylator MACD (okno pierwsze od góry). W oknie drugim zamieszczona została transformata Fishera z oscylatora MACD, a w trzecim transformata Fishera (30 dniowa) ceny akcji KGHM. W oknie czwartym umieszczony został akcjogram KGHM.Odwrotna transformata Fishera (OTF)
Rozwiązanie równania 1 ze względu na x daje zależność:
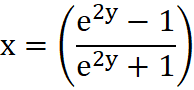
Równanie 2
Jeśli teraz sygnał x ma być sygnałem wejściowym, a y wyjściowym to równanie 2 przyjmuje postać (zamiana zmiennych x z y):
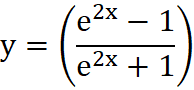
Równanie 3
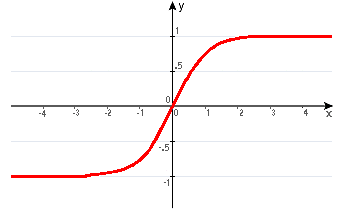
Rysunek 5. Sygnał wyjściowy w odwrotnej transformacie Fishera
Źródło: opracowanie własne.
W przypadku odwrotnej transformaty Fishera dla sygnału wejściowego z przedziału <-0,5; 0,5>, sygnał wyjściowy jest praktycznie równy wielkości sygnału wejściowego. Jednak w przypadku stanów ekstremalnych tj. dla x<-2 i x>2, wartość sygnału wyjściowego jest równa odpowiednio -1 i 1. Główną zaletą odwrotnej transformaty Fishera jest fakt, że sygnał wyjściowy przybiera z dużym prawdopodobieństwem jedną z wartości: -1 lub 1. Bipolarność odwrotnej transformaty Fishera czyni ją idealnym narzędziem wykorzystywanym w analizie technicznej do generowania wskazań kupna lub sprzedaży.
Odwrotna transformata Fishera i oscylator RSI
Jednym z najbardziej popularnych oscylatorów AT jest oscylator siły relatywnej RSI. Konstrukcja oscylatora powoduje, że porusza się on w przedziale od zera do 100. Jeśli od wartości oscylatora odejmiemy najpierw 50 punktów, a następnie wynik przemnożymy przez jedną dziesiątą:
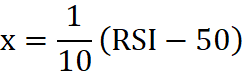
Równanie 4
to wynik będzie należał do przedziału <-5; 5>, a wartość sygnału wyjściowego y do przedziału <-1; 1>. W następnej kolejności przy pomocy przekształcenia (normalizacja):
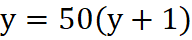
Równanie 5
powracamy do skali od zera do 100, tak aby łatwiej było narysować przetransformowany i znormalizowany oscylator RSI.
Tabela 1. Przykład obliczenia oscylatora RSI z wykorzystaniem odwrotnej transformaty Fishera
100
X
Y
Znormalizowany RSI po odwrotnej transformacie
5
1.000
100
90
X
Y
Znormalizowany RSI po odwrotnej transformacie
4
0.999
99.9
80
X
Y
Znormalizowany RSI po odwrotnej transformacie
3
0.995
99.8
70
X
Y
Znormalizowany RSI po odwrotnej transformacie
2
0.964
98.2
65
X
Y
Znormalizowany RSI po odwrotnej transformacie
1.5
0.905
95.3
60
X
Y
Znormalizowany RSI po odwrotnej transformacie
1
0.762
88.1
55
X
Y
Znormalizowany RSI po odwrotnej transformacie
.5
0.462
73.1
50
X
Y
Znormalizowany RSI po odwrotnej transformacie
0
0.000
50
45
X
Y
Znormalizowany RSI po odwrotnej transformacie
-0.5
-0.462
26.9
40
X
Y
Znormalizowany RSI po odwrotnej transformacie
-1
-0.762
11.9
35
X
Y
Znormalizowany RSI po odwrotnej transformacie
-1.5
-0.905
4.7
30
X
Y
Znormalizowany RSI po odwrotnej transformacie
-2
-0.964
1.8
20
X
Y
Znormalizowany RSI po odwrotnej transformacie
-3
-0.995
0.2
10
X
Y
Znormalizowany RSI po odwrotnej transformacie
-4
-0.999
0.1
0
X
Y
Znormalizowany RSI po odwrotnej transformacie
-5
-1.000
0
| Wartość RSI | X | Y | Znormalizowany RSI po odwrotnej transformacie |
|---|---|---|---|
| 100 | 5 | 1.000 | 100 |
| 90 | 4 | 0.999 | 99.9 |
| 80 | 3 | 0.995 | 99.8 |
| 70 | 2 | 0.964 | 98.2 |
| 65 | 1.5 | 0.905 | 95.3 |
| 60 | 1 | 0.762 | 88.1 |
| 55 | .5 | 0.462 | 73.1 |
| 50 | 0 | 0.000 | 50 |
| 45 | -0.5 | -0.462 | 26.9 |
| 40 | -1 | -0.762 | 11.9 |
| 35 | -1.5 | -0.905 | 4.7 |
| 30 | -2 | -0.964 | 1.8 |
| 20 | -3 | -0.995 | 0.2 |
| 10 | -4 | -0.999 | 0.1 |
| 0 | -5 | -1.000 | 0 |
żródło: opracowanie własne.
Wartości oscylatora RSI większe od 60 zostaną przetransformowane do przedziału <88; 100>, zaś wartości RSI mniejsze od 40 do przedziału <0;12>. Wartości RSI z przedziału <40;60> zostaną narysowane jako ostre przejście między stanem niskim i wysokim oscylatora RSI.
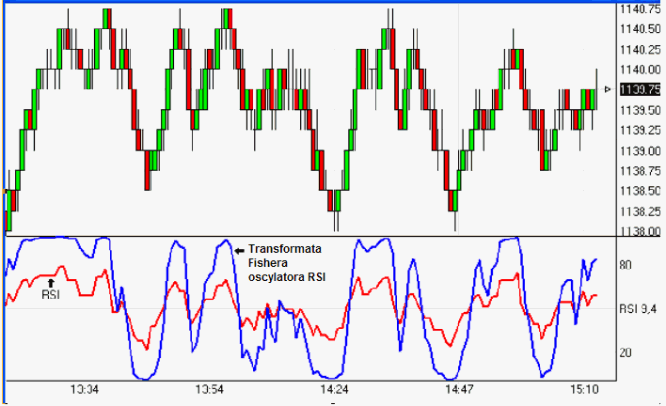
Rysunek 6. Ilustracja wzajemnego położenia oscylatora RSI i jego odwrotnej transformaty Fishera na przykładzie indeksu S&P (notowania intraday)
Źródło: opracowanie własne.
Analogiczną operacją możemy przeprowadzić dla średniej ruchomej z RSI - odwrotnej transformacie Fishera poddajemy średnią ruchomą z oscylatora. Punkty zwrotne są nadal bardzo wyraźnie zaznaczone. Na rys. 7 przedstawione zostało wykorzystanie odwrotnej transformaty Fishera w dwugodzinnym trendzie bocznym. Stany wykupienia i wyprzedania odwrotnej transformaty stanowią doskonałe momenty wejścia na rynek lub zamknięcia pozycji długiej.
Rysunek 7. Ilustracja wzajemnego położenia oscylatora RSI i odwrotnej transformaty Fishera z 9 sesyjnej średniej z RSI na przykładzie indeksu S&P (notowania intraday)
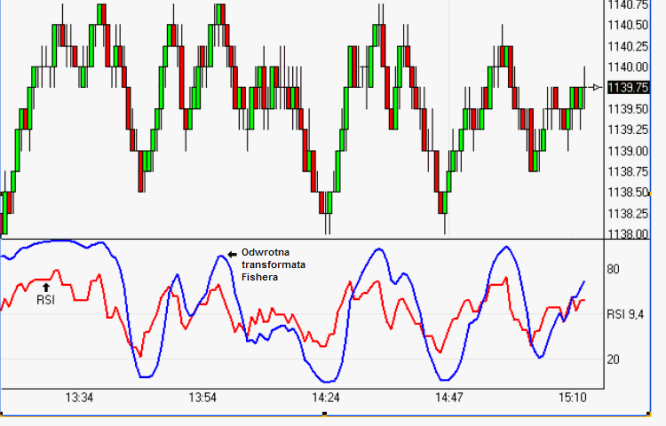
Źródło: opracowanie własne.
Odwrotna transformata Fishera bazująca na RSI może zostać wykorzystana do budowy prostego systemu transakcyjnego:
- Sygnał kupna (pozycja długa - Buy) - OTF przekracza poziom 50 pkt w górę,
- Sygnał sprzedaży (zamknięcie pozycji długiej - Exit Long) - kiedy OTF przebywa powyżej 80 pkt a następnie przełamuje poziom 80 pkt od góry
- Sygnał sprzedaży (pozycja krótka - Sell) - OTF przebija poziom 50 pkt w dół.
- Sygnał kupna (zamknięcie pozycji krótkiej - Exit short) - kiedy OTF przebywa poniżej a następnie przełamuje poziom 20 pkt od dołu
Przykład zastosowania takiego systemu transakcyjnego został przedstawiony na rys. 8.
Rysunek 8. Zastosowanie systemy transakcyjnego z OTF w notowaniach intradayowych w przypadku indeksu S&P
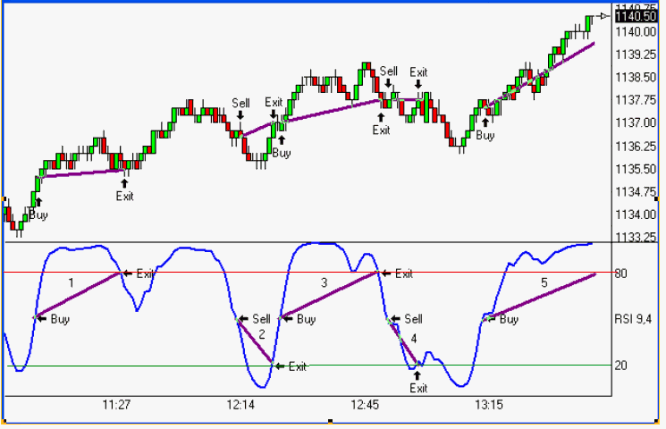
Źródło: opracowanie własne.
Kolejną modyfikacją równania nr 3 i nr 4 może być:
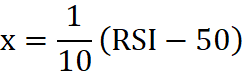
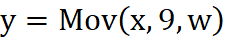
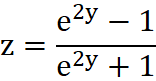
Równanie 6
gdzie:
- y - oznacza średnią ruchomą 9 sesyjną ze zmiennej x liniowo ważoną ostatnią ceną[5]
- z - jest sygnałem wyjściowym ze zmodyfikowanego w ten sposób oscylatora RSI
Rysunek 9. Zastosowanie systemu transakcyjnego z odwrotną transformatą Fishera na przykładzie akcji KGHM
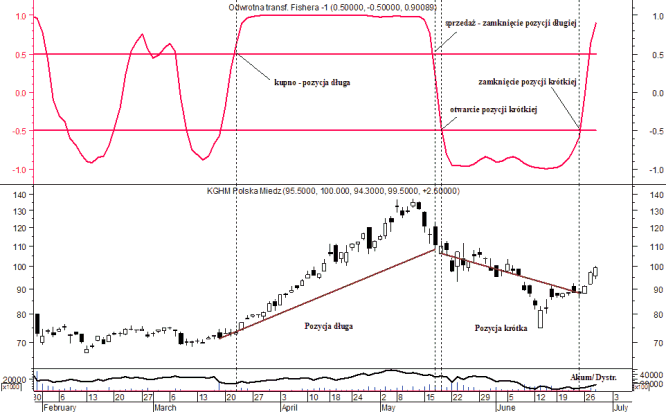
Źródło: opracowanie własne.
W ten sposób możemy stworzyć kolejny system transakcyjny przy wykorzystaniu odwrotnej transformaty Fishera bazująca na RSI:
- Sygnał kupna (pozycja długa - Buy) - OTF przekracza poziom 0,5 pkt od dołu w górę,
- Sygnał sprzedaży (zamknięcie pozycji długiej - Exit Long) - kiedy OTF przebija od góry w dół poziom 0,5
- Sygnał sprzedaży (pozycja krótka - Sell) - OTF przebija poziom -0,5 pkt od góry w dół.
- Sygnał kupna (zamknięcie pozycji krótkiej - Exit short) - kiedy OTF przebija poziom -0,5 od dołu w górę.
Zastosowanie odwrotnej transformaty Fishera z innymi wskaźnikami
Odwrotna transformata Fishera może być wykorzystywana także z innym wskaźnikami analizy technicznej. Jako przykład podajmy jej wykorzystanie z oscylatorem Cyber cycles[6]. W skrócie dowolny szereg czasowy można rozłożyć na składową trendu i składową cykliczną.
Rysunek 10. Przykład zastosowania odwrotnej transformaty Fishera w przypadku oscylatora Cyber cycle
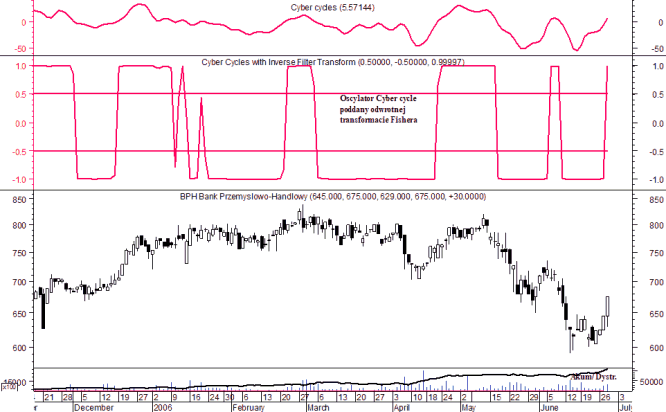
Źródło: opracowanie własne.
Głównym zadaniem oscylatora Cyber cycle jest znalezienie komponentów cyklicznych przy wykorzystaniu procesu filtrowania[7]. Na wykresie oscylatora (pierwsze górne okno na rys. 10) widoczne są cykliczne zmiany kierunku charakteryzujące się różnymi amplitudami. Zastosowanie odwrotnej transformaty Fishera uwypukla zmiany kierunku oscylatora i pozwala na generowanie bardziej precyzyjnych sygnałów zmiany trendu: przełamanie przez OTF poziomów -0,5 i 0,5 pkt - drugie okno od góry na rys. 10. W przypadku przedstawionym na rys.10 jako linie sygnalne odwrotnej transformaty Fishera z oscylatora Cyber cycle użyte zostały poziomy -0,5 i 0,5.
Podsumowanie
Rozwój technologii komputerowych i zwiększenie możliwości obliczeniowych powoduje sięganie przez analizę techniczną do coraz bardziej skomplikowanych narzędzi. Jednym z nich jest proces obliczania odwrotnej transformaty Fishera dla cen aktywów z wybranego okna czasowego. Wykorzystanie statystycznych właściwości tej metody pozwala na zastosowanie jej do binarnego generowania wskazań kupna lub sprzedaży analizowanego aktywu oraz wprzęgnięcie tej metody do budowy systemów transakcyjnych.
Bibliografia
- Achelis S. "Analiza techniczna od A do Z", Oficyna Wydawnicza LT&P, Warszawa 1998.
- Ehlers J. "Using the Fisher Transform", Technical Analysis of Stocks & Commodities, November 2002.
- Ehlers J. "Cybernetic Analysis For Stock And Futures", John Willey & Sons, New York 2004.
- Ehlers J. "The Inverse Fisher Transform", Technical Analysis of Stocks & Commodities, May 2004.
- Murphy J. "Analiza techniczna", WIG-PRESS, Warszawa 1999.
- Nowakowski J., Borowski K. "Zastosowanie teorii Fischera i Carolana na rynku kapitałowym", Difin, Warszawa 2005.
Strony internetowe:
http://www.prophet.net/analyze/popglossary.jsp?studyid=CCO (odsłona z dnia 29.06.2006).
Referencje
[1] W przypadku transformaty Fishera zastosowanie w analizie technicznej mają raczej ceny aktywów, a nie ich zmiany.
[2] Ehlers J. "The Inverse Fisher Transform", Technical Analysis of Stocks & Commodities, May 2004.
[3] Ehlers J. "Using the Fisher Transform", Technical Analysis of Stocks & Commodities, November 2002.
[4] Omówienie konstrukcji i zastosowania w analizie technicznej podstawowych oscylatorów i wskaźników (MACD, ROC i RSI) można znaleźć m.in. w:
- Murphy J. "Analiza techniczna", WIG-PRESS, Warszawa 1999
- Achelis S. "Analiza techniczna od A do Z", Oficyna Wydawnicza LT&P, Warszawa 1998.
[5] Liniowa ważona średnia ruchoma przypisuje większą wagę ostatnim cenom, a mniejszą wcześniejszym. Oblicza się ją mnożąc cenę (najczęściej zamknięcia) przez określoną wagę. Poniżej przedstawiony został sposób obliczenia średniej ważonej pięciosesyjnej:
1
Waga
Cena
Iloczyn ceny i wagi
1
25
25
2
Waga
Cena
Iloczyn ceny i wagi
2
26
52
3
Waga
Cena
Iloczyn ceny i wagi
3
28
84
4
Waga
Cena
Iloczyn ceny i wagi
4
25
100
5
Waga
Cena
Iloczyn ceny i wagi
5
29
145
Razem
Waga
Cena
Iloczyn ceny i wagi
15
133
406
| Dzień | Waga | Cena | Iloczyn ceny i wagi |
|---|---|---|---|
| 1 | 1 | 25 | 25 |
| 2 | 2 | 26 | 52 |
| 3 | 3 | 28 | 84 |
| 4 | 4 | 25 | 100 |
| 5 | 5 | 29 | 145 |
| Razem | 15 | 133 | 406 |
Następnie dzieląc sumę wszystkich iloczynów cen i wag tj. 406 przez sumę wag tj. 15 otrzymujemy średnią liniowo ważoną pięcioseryjną - 27,067.
Ujęcie matematyczne takiego procesu dla średniej N sesyjnej możemy przedstawić jako:
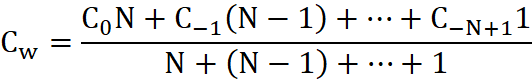
gdzie:
- CW - średnia liniowo ważona z okresu N sesji
- C0 - cena na zakończenie ostatniej sesji
- C-1 - cena na zakończeni poprzedniej sesji
- C-N+1 - cena zamknięcia N sesji temu
Więcej na temat zastosowania liniowo ważonej średniej ruchomej i jej zastosowania w analizie technicznej można znaleźć m.in. w: Nowakowski J., Borowski K. "Zastosowanie teorii Fischera i Carolana na rynku kapitałowym", Difin, Warszawa 2005.
[6] Dokładne omówienia konstrukcji tego oscylatora można znaleźć m.in. na stronie internetowej: http://www.prophet.net/analyze/popglossary.jsp?studyid=CCO (odsłona z dnia 29.06.2006).
[7] Oscylator Cyber cycles stanowi narzędzie analizy technicznej wykorzystujące tzw. analizę spektralną podobnie jak transformata Fouriera.
Niniejszy materiał, przygotowany przez DM BOŚ S.A. ma charakter wyłącznie informacyjny, prezentowany jest w celach edukacyjnych i nie stanowi porady prawnej oraz nie jest rekomendacją osobistą w ramach świadczenia usługi doradztwa inwestycyjnego zgodnie z przepisami prawa. DM BOŚ S.A. nie udziela gwarancji dokładności, aktualności, oraz kompletności niniejszych informacji. Zaleca się przeprowadzenie we własnym zakresie niezależnego przeglądu informacji z niniejszego materiału.


